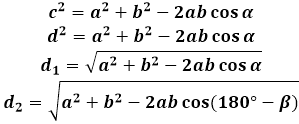Przekątne Równoległoboku

Równoległobok to czworokąt, którego przeciwległe boki są równoległe i równe z definicji. W konsekwencji, przeciwległe kąty równoległoboku również będą sobie równe, a ponieważ suma wszystkich kątów w czworokącie wynosi 360 stopni, można stwierdzić, że suma dwóch kolejnych kątów wynosi 180 stopni. Ta właściwość odegra istotną rolę w znalezieniu przekątnych równoległoboku, biorąc pod uwagę, że mają one różne długości.

Ponieważ każda przekątna równoległoboku dzieli go na dwa równe trójkąty, ich właściwości zostaną użyte do wyprowadzenia wzoru na przekątną równoległoboku.

W dowolnym trójkącie, kąt i bok naprzeciwko niego są proporcjonalne do siebie. Dla równoległoboku oznacza to, że dłuższa przekątna leży naprzeciw kąta rozwartokątnego, a krótsza przekątna - naprzeciw kąta ostrego. Biorąc pod uwagę, że boki trójkątów utworzonych przez przekątne są takie same - są to boki równoległoboku, miara kątowa kąta między tymi bokami określa długość przekątnej, obliczoną według wzoru. Innymi słowy, jeśli do wzoru na przekątną zostanie podstawiona wartość kąta ostrego równoległoboku, kalkulator obliczy długość krótkiej przekątnej, a jeśli wartość kąta rozwartokątnego - długiej.

Aby przejść z jednego kąta na inny, używa się różnicy 180 stopni i danego kąta, dzięki czemu kalkulator może jednocześnie obliczyć obie przekątne.

α=180°-β

Aby wyprowadzić wzór na przekątną równoległoboku, stosuje się twierdzenie cosinusów w trójkącie utworzonym przez przekątną z bokami. W dowolnym z takich trójkątów, przekątna jest bokiem naprzeciw kąta równoległoboku, a zatem jej kwadrat równa się sumie kwadratów dwóch pozostałych boków trójkąta (równoległoboku, w tym przypadku) minus dwa razy iloczyn tych samych boków razy cosinus danego kąta. Aby znaleźć długość przekątnej równoległoboku, kalkulator oblicza pierwiastek kwadratowy z tego wyrażenia.