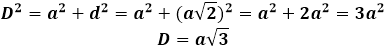Przekątna Sześcianu

Sześcian jest podstawowym ciałem geometrycznym, jeśli chodzi o objętość i ciała przestrzenne. Nic dziwnego, że trzecia potęga, która jest uzyskiwana przez pomnożenie trzech identycznych liczb razem (jak przy znajdowaniu objętości sześcianu - trzy jego identyczne wymiary) jest nazwana na jego cześć.

Głównym i jedynym parametrem sześcianu jest jego krawędź a, ponieważ wszystkie krawędzie sześcianu są przystające i reprezentują zarówno długość, szerokość, jak i wysokość. W związku z tym tylko jedna wartość określa wszystkie możliwe cechy sześcianu związane z jego wymiarami.

Oprócz krawędzi, wierzchołki sześcianu mogą być połączone przekątnymi. Przekątne mogą przechodzić przez powierzchnie sześcianu, w takim przypadku będą one po prostu przekątnymi podstawy lub przekątnymi kwadratu w płaszczyźnie, lub przekątne mogą być rysowane wewnątrz samego sześcianu, łącząc przeciwległe podstawy w skrajnych punktach (wierzchołków).

Aby znaleźć przekątną sześcianu przez jego krawędź, najpierw należy wykonać dodatkowe konstrukcje w postaci przekątnej jednej z połączonych podstaw, wtedy przekątna sześcianu staje się przeciwprostokątną nowo utworzonego trójkąta prostokątnego, którego przyprostokątnymi są krawędź sześcianu i przekątna podstawy. Jeśli krawędź sześcianu jest znana z warunków zadania, to przekątną kwadratu w podstawie należy najpierw obliczyć za pomocą wzoru: d=a√2

Wtedy przekątna sześcianu może być wyrażona przez twierdzenie Pitagorasa, i przyjmie następującą formę: