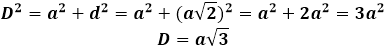Diagonal do Cubo

Um cubo é um corpo geométrico básico quando se trata de volume e corpos volumétricos. Não surpreende que a terceira potência, que é obtida multiplicando três números idênticos juntos (como ao encontrar o volume de um cubo - três das suas medidas idênticas) é nomeada em sua honra.

O principal e único parâmetro do cubo é a sua aresta a, uma vez que todas as arestas de um cubo são congruentes e representam tanto o comprimento, a largura e a altura. Assim, apenas um valor determina todas as possíveis características do cubo relacionadas com as suas dimensões.

Além das arestas, os vértices do cubo podem ser conectados por diagonais. As diagonais podem passar pelas faces do cubo, caso em que serão simplesmente a diagonal da base ou a diagonal quadrada no plano, ou as diagonais podem ser traçadas dentro do próprio cubo, conectando bases opostas em pontos extremos (vértices).

Para encontrar a diagonal do cubo através da sua aresta, primeiro é necessário fazer uma construção adicional na forma da diagonal de uma das bases conectadas, então a diagonal do cubo torna-se a hipotenusa do triângulo retângulo recém-formado, cujas pernas são a aresta do cubo e a diagonal da base. Se a aresta do cubo é dada pelas condições do problema, então a diagonal do quadrado na base deve primeiro ser calculada usando a fórmula: d=a√2

Então a diagonal do cubo pode ser expressa através de o teorema de Pitágoras, e ela tomará a seguinte forma: