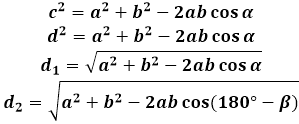Diagonály rovnobežníka

Paralelogram je štvoruholník, ktorého protiľahlé strany sú rovnobežné a rovnaké podľa definície. Následne, protiľahlé uhly paralelogramu budú tiež rovnaké, a keďže súčet všetkých uhlov v štvoruholníku je 360 stupňov, možno dospieť k záveru, že súčet dvoch po sebe nasledujúcich uhlov bude 180 stupňov. Táto vlastnosť bude zohrávať významnú úlohu pri hľadaní diagonál paralelogramu, vzhľadom na to, že majú rôzne dĺžky.

Pretože každá diagonála paralelogramu ho delí na dva rovnaké trojuholníky, ich vlastnosti budú použité na odvodenie vzorca pre diagonálu paralelogramu.

V ľubovoľnom trojuholníku sú uhol a strana oproti nemu navzájom úmerné. Pre paralelogram to znamená, že dlhšia diagonála bude ležať oproti tupému uhlu a kratšia diagonála - oproti ostrému uhlu. Vzhľadom na to, že strany trojuholníkov, ktoré vznikajú diagonálami, sú rovnaké - to sú strany paralelogramu, stupňová miera uhla medzi týmito stranami určuje dĺžku diagonály, vypočítanú podľa vzorca. Inými slovami, ak je do vzorca pre diagonálu dosadená hodnota ostrého uhla paralelogramu, kalkulačka vypočíta dĺžku krátkej diagonály, a ak je dosadená hodnota tupého uhla - dlhú.

Na prechod z jedného uhla na druhý sa používa rozdiel 180 stupňov a daný uhol, týmto spôsobom kalkulačka dokáže naraz vypočítať obe diagonály.

α=180°-β

Na odvodenie vzorca pre diagonálu paralelogramu sa používa kosínová veta v trojuholníku, ktorý vzniká diagonálou so stranami. V ľubovoľnom z týchto trojuholníkov je diagonála stranou oproti uhlu paralelogramu a jej štvorcom sa rovná súčtu štvrtcov dvoch ďalších strán trojuholníka (paralelogramu, v tomto prípade) mínus dvakrát súčin tých istých strán kosínom daného uhla. Na nájdenie dĺžky diagonály paralelogramu kalkulačka vypočíta druhú odmocninu tohto výrazu.