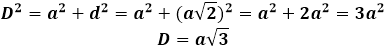Diagonála kocky

Kocka je základné geometrické teleso, keď ide o objem a objemové telesá. Nie je prekvapujúce, že tretia mocnina, ktorá sa získa násobením troch identických čísel spolu (ako pri nájdení objemu kocky - tri jeho identické rozmery) je pomenovaná na jeho počesť.

Hlavným a jediným parametrom kocky je jej hrana a, keďže všetky hrany kocky sú zhodné a predstavujú zároveň dĺžku, šírku a výšku. Preto len jedna hodnota určuje všetky možné charakteristiky kocky súvisiace s jej rozmermi.

Okrem hrán môžu byť vrcholy kocky spojené diagonálami. Diagonály môžu prechádzať cez tváre kocky, v takom prípade budú jednoducho diagonálou základne alebo diagonálou štvorca v rovine, alebo môžu byť diagonály nakreslené vo vnútri kocky samotnej, spájajúc protilehlé základne v extrémnych bodoch (vrcholov).

Na nájdenie diagonály kocky cez jej hranu je najprv potrebné urobiť dodatočnú konštrukciu vo forme diagonály jednej z pripojených základní, potom sa diagonála kocky stane preponou novovytvoreného pravouhlého trojuholníka, ktorého katetmi sú hrana kocky a diagonála základne. Ak je hrana kocky daná podmienkami úlohy, potom je najprv potrebné vypočítať diagonálu štvorca na základni pomocou vzorca: d=a√2

Potom môže byť diagonála kocky vyjadrená cez Pytagorovu vetu, a nadobudne nasledujúcu formu: