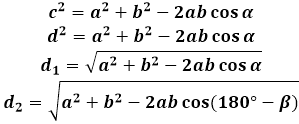Diagonale paralelograma

Paralelogram je štirikotnik, katerega nasprotne stranice so vzporedne in enake po definiciji. Posledično bodo nasprotni koti paralelograma bodo tudi enaki drug drugemu, in ker je vsota vseh kotov v štirikotniku 360 stopinj, lahko sklepamo, da bo vsota dveh zaporednih kotov 180 stopinj. Ta lastnost bo igrala pomembno vlogo pri iskanju diagonal paralelograma, saj so različnih dolžin.

Ker vsaka diagonala paralelograma deli na dva enaka trikotnika, bodo njihove lastnosti uporabljene za izpeljavo formule za diagonalo paralelograma.

V vsakem trikotniku sta kot in stranica nasproti njega proporcionalna drug drugemu. Za paralelogram to pomeni, da bo daljša diagonala ležala nasproti topemu kotu, krajša diagonala pa nasproti ostremu kotu. Upoštevajoč, da so stranice trikotnikov, ki jih tvorijo diagonale, enake - to so stranice paralelograma, meri kota med temi stranicami določajo dolžino diagonale, izračunane po formuli. Z drugimi besedami, če vrednost ostrega kota paralelograma nadomestimo v formulo za diagonalo, bo kalkulator izračunal dolžino krajše diagonale, in če nadomestimo vrednost topega kota - daljše.

Za prehod z enega kota na drugega se uporablja razlika 180 stopinj in danega kota, tako da lahko kalkulator hkrati izračuna obe diagonali.

α=180°-β

Za izpeljavo formule za diagonalo paralelograma se uporablja kosinusni izrek v trikotniku, ki ga tvori diagonala s stranicami. V katerem koli od takih trikotnikov je diagonala stranica nasproti kota paralelograma in ustrezno je njen kvadrat enak vsoti kvadratov drugih dveh stranic trikotnika (paralelograma, v tem primeru) minus dvakratni produkt istih stranic s kosinusom danega kota. Za iskanje dolžine diagonale paralelograma kalkulator izračuna kvadratni koren tega izraza.