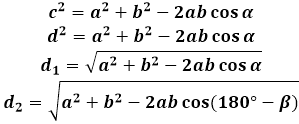Dijagonale paralelograma

Paralelogram je četvorougao čije su suprotne stranice paralelne i jednake po definiciji. Posledično, suprotni uglove paralelograma će takođe biti jednaki međusobno, a pošto je zbir svih uglova u četvorouglu 360 stepeni, može se zaključiti da će zbir dva uzastopna ugla biti 180 stepeni. Ovo svojstvo će igrati značajnu ulogu u pronalaženju dijagonala paralelograma, s obzirom da su različitih dužina.

Pošto svaka dijagonala paralelograma deli ga na dva jednaka trougla, njihova svojstva će se koristiti za izvođenje formule za dijagonalu paralelograma.

U bilo kojem trouglu, ugao i stranica naspram njega su proporcionalni međusobno. Za paralelogram, to znači da će duža dijagonala ležati naspram tupog ugla, a kraća dijagonala - naspram oštrog ugla. S obzirom da su stranice trouglova formiranih dijagonalama iste - to su stranice paralelograma, stepen mjera ugla između ovih stranica određuje dužinu dijagonale, izračunatu formulom. Drugim rečima, ako se vrednost oštrog ugla paralelograma zameni u formulu za dijagonalu, kalkulator će izračunati dužinu kratke dijagonale, a ako se zameni vrednost tupog ugla - duge.

Da biste prešli sa jednog ugla na drugi, koristi se razlika od 180 stepeni i datog ugla, tako da kalkulator može istovremeno izračunati obe dijagonale.

α=180°-β

Da bi se izvela formula za dijagonalu paralelograma, koristi se kosinusna teorema u trouglu formiranom dijagonalom sa stranicama. U bilo kojem od takvih trouglova, dijagonala je stranica naspram ugla paralelograma, i u skladu s tim, njen kvadrat je jednak zbiru kvadrata dveju drugih stranica trougla (paralelograma, u ovom slučaju) minus dva puta proizvod istih stranica sa kosinusom datog ugla. Da bi se pronašla dužina dijagonale paralelograma, kalkulator računa kvadratni koren ovog izraza.