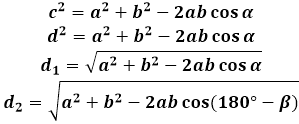Parallellogramdiagonaler

En parallellogram är en fyrhörning vars motsatta sidor är parallella och lika enligt definitionen. Följaktligen, de motsatta vinklarna av parallellogrammet kommer också att vara lika med varandra, och eftersom summan av alla vinklar i en fyrhörning är 360 grader, kan det dras slutsatsen att summan av två på varandra följande vinklar kommer att vara 180 grader. Denna egenskap kommer att spela en betydande roll i att hitta parallellogrammets diagonaler, med tanke på att de är av olika längder.

Eftersom varje diagonal av en parallellogram delar den i två lika trianglar, kommer deras egenskaper att användas för att härleda formeln för parallellogrammets diagonal.

I en valfri triangel är vinkeln och sidan mittemot den proportionella mot varandra. För en parallellogram innebär detta att den längre diagonalen kommer att ligga mittemot den trubbiga vinkeln, och den kortare diagonalen - mittemot den spetsiga vinkeln. Med tanke på att sidorna av trianglarna som bildas av diagonalerna är desamma - dessa är parallellogrammets sidor, bestämmer gradmåttet av vinkeln mellan dessa sidor längden på diagonalen, beräknad med formeln. Med andra ord, om värdet av parallellogrammets spetsiga vinkel sätts in i formeln för diagonalen, kommer kalkylatorn att beräkna längden på den korta diagonalen, och om värdet av den trubbiga vinkeln sätts in - den långa.

För att växla från en vinkel till en annan används skillnaden på 180 grader och den givna vinkeln, så att kalkylatorn samtidigt kan beräkna båda diagonalerna.

α=180°-β

För att härleda formeln för parallellogrammets diagonal används cosinussatsen i triangeln som bildas av diagonalen med sidorna. I någon av sådana trianglar är diagonalen sidan mittemot parallellogrammets vinkel, och följaktligen är dess kvadrat lika med summan av kvadraterna av de två andra sidorna av triangeln (av parallellogrammet, i detta fall) minus dubbla produkten av samma sidor med cosinus av den givna vinkeln. För att hitta längden på parallellogrammets diagonal, beräknar kalkylatorn kvadratroten av detta uttryck.