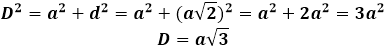Kubdiagonal

En kub är en grundläggande geometrisk kropp när det gäller volym och volymetriska kroppar. Inte överraskande, den tredje potensen, som erhålls genom att multiplicera tre identiska nummer tillsammans (som när man beräknar volymen av en kub - tre av dess identiska mått) är uppkallad efter dess ära.

Den huvudsakliga och enda parametern för kuben är dess kant a, eftersom alla kanter av en kub är kongruenta och representerar både längd, bredd och höjd. Följaktligen bestämmer endast ett värde alla möjliga egenskaper hos kuben relaterade till dess dimensioner.

Förutom kanterna kan kubens hörn förbindas av diagonaler. Diagonaler kan passera genom kubens ytor, i vilket fall de helt enkelt är basdiagonalen eller kvadratdiagonalen i planet, eller diagonalerna kan dras inuti själva kuben, förbindande motsatta baser vid extrema punkter (hörn).

För att hitta kubdiagonalen genom dess kant, måste du först göra en ytterligare konstruktion i form av diagonalen av en av de anslutna baserna, då blir kubdiagonalen hypotenusan i den nybildade rätvinkliga triangeln, vars ben är kubens kant och basdiagonalen. Om kubens kant är given av problemets villkor, måste kvadratdiagonalen vid basen först beräknas med hjälp av formeln: d=a√2

Då kan kubdiagonalen uttryckas genom Pythagoras sats, och den kommer att anta följande form: