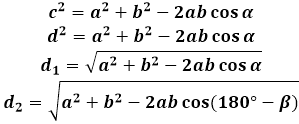เส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนาน

รูปสี่เหลี่ยมด้านขนานคือสี่เหลี่ยมมุมฉากที่มีด้านตรงข้ามขนานกันและเท่ากันตามนิยาม ดังนั้น มุมของรูปสี่เหลี่ยมด้านขนาน จะเท่ากันด้วย และเนื่องจากผลรวมของมุมทั้งหมดในสี่เหลี่ยมมุมฉากคือ 360 องศา จึงสามารถสรุปได้ว่าผลรวมของมุมสองมุมต่อเนื่องกันจะเป็น 180 องศา คุณสมบัตินี้จะมีบทบาทสำคัญในการหาสูตรสำหรับเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนาน โดยพิจารณาว่าพวกมันมีความยาวต่างกัน

เนื่องจากเส้นทแยงมุมแต่ละเส้นของรูปสี่เหลี่ยมด้านขนานแบ่งมันออกเป็นสองสามเหลี่ยมที่เท่ากัน คุณสมบัติของพวกมันจะถูกใช้เพื่ออนุมานสูตรสำหรับเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนาน

ในสามเหลี่ยมใดๆ มุมและด้านตรงข้ามของมันมีสัดส่วนต่อกัน สำหรับรูปสี่เหลี่ยมด้านขนาน หมายความว่าเส้นทแยงมุมที่ยาวกว่าจะอยู่ตรงข้ามมุมป้าน และเส้นทแยงมุมที่สั้นกว่า - ตรงข้ามมุมแหลม โดยพิจารณาว่าด้านของสามเหลี่ยมที่เกิดจากเส้นทแยงมุมคือด้านของรูปสี่เหลี่ยมด้านขนาน มาตรวัดมุมระหว่างด้านเหล่านี้กำหนดความยาวของเส้นทแยงมุม คำนวณโดยสูตร กล่าวอีกนัยหนึ่ง ถ้าค่าองศามุมแหลมของรูปสี่เหลี่ยมด้านขนานถูกแทนในสูตรสำหรับเส้นทแยงมุม เครื่องคำนวณจะคำนวณความยาวของเส้นทแยงมุมสั้น และถ้ามุมป้าน - เส้นทแยงมุมยาว

เพื่อสลับจากมุมหนึ่งไปยังอีกมุมหนึ่ง ใช้ผลต่างของ 180 องศาและมุมที่กำหนด จึงสามารถคำนวณเส้นทแยงมุมทั้งสองพร้อมกัน

α=180°-β

เพื่อให้ได้สูตรสำหรับเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนาน ใช้ทฤษฎีโคไซน์ในสามเหลี่ยมที่เกิดจากเส้นทแยงมุมและด้าน ในสามเหลี่ยมดังกล่าว เส้นทแยงมุมเป็นด้านตรงข้ามมุมของรูปสี่เหลี่ยมด้านขนาน และดังนั้นกำลังสองเท่ากับผลรวมของกำลังสองของสองด้านอื่นๆ ของสามเหลี่ยม (ของรูปสี่เหลี่ยมด้านขนาน ในกรณีนี้) ลบด้วยสองเท่าของผลคูณของด้านเดียวกันกับโคไซน์ของมุมที่กำหนด เพื่อหาความยาวของเส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนาน เครื่องคำนวณจะคำนวณรากที่สองของนิพจน์นี้