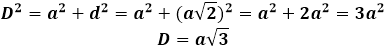เส้นทแยงมุมของลูกบาศก์
ลูกบาศก์เป็นรูปทรงเรขาคณิตพื้นฐานเมื่อพูดถึงปริมาตรและรูปทรงสามมิติ ไม่แปลกใจเลยที่พลังที่สามซึ่งได้มาจากการคูณตัวเลขที่เหมือนกันสามตัวเข้าด้วยกัน (เช่นเมื่อหาปริมาตร ของลูกบาศก์ - สามในมาตรวัดที่เหมือนกัน) ถูกตั้งชื่อตามเกียรติของมัน
พารามิเตอร์หลักและเดียวของลูกบาศก์คือขอบของมัน a, เนื่องจากขอบทั้งหมดของลูกบาศก์มีความยาวเท่ากันและเป็นทั้งความยาว ความกว้าง และความสูง ดังนั้นค่าหนึ่งค่าจะกำหนดลักษณะทั้งหมดของลูกบาศก์ที่เกี่ยวข้องกับขนาดของมัน
นอกจากขอบแล้ว จุดยอดของลูกบาศก์สามารถเชื่อมต่อด้วยเส้นทแยงมุม เส้นทแยงมุมสามารถผ่านใบหน้าของลูกบาศก์ ซึ่งในกรณีนี้จะเป็นเพียงเส้นทแยงมุมของฐานหรือเส้นทแยงมุมของจัตุรัสในระนาบ หรือเส้นทแยงมุมสามารถวาดภายในลูกบาศก์เอง เชื่อมต่อฐานตรงข้ามที่จุดปลาย (จุดยอด).
เพื่อหาความยาวเส้นทแยงมุมของลูกบาศก์ผ่านขอบของมัน คุณต้องสร้างเส้นทแยงมุมเพิ่มเติมในรูปของเส้นทแยงมุมของฐานที่เชื่อมต่อกัน จากนั้นเส้นทแยงมุมของลูกบาศก์จะกลายเป็นเส้นทแยงมุมใหญ่ของสามเหลี่ยมมุมฉากที่สร้างขึ้นใหม่ ขาของมันคือขอบของลูกบาศก์และเส้นทแยงมุมของฐาน หากขอบของลูกบาศก์ถูกกำหนดโดยเงื่อนไขของปัญหา เส้นทแยงมุมของฐานต้องคำนวณโดยใช้สูตรก่อน: d=a√2
จากนั้นเส้นทแยงมุมของลูกบาศก์สามารถแสดงออกผ่าน ทฤษฎีบทพีทาโกรัส, และจะมีลักษณะดังนี้: