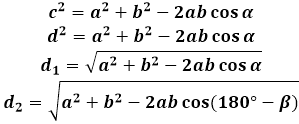Paralelkenar Köşegenleri

Bir paralelkenar, tanım gereği karşıt kenarları paralel ve eşit olan bir dörtgendir. Dolayısıyla, karşıtparalelkenarın açıları birbirine eşit olacak ve çünkü dörtgenin tüm açıları toplamı 360 derece olduğundan, ardışık iki açının toplamının 180 derece olacağı sonucuna varılabilir. Bu özellik, köşegenlerin farklı uzunluklara sahip olduğunu göz önünde bulundurarak, paralelkenarın köşegenlerini bulmada önemli bir rol oynayacaktır.

Her paralelkenarın köşegeni onu iki eşit üçgene böldüğü için, paralelkenarın köşegeninin formülünü türetmek için bu özellikler kullanılacaktır.

Her üçgende, açı ve karşısındaki kenar birbirine orantılıdır. Bir paralelkenar için bu, daha uzun köşegenin geniş açının karşısında, daha kısa köşegenin ise dar açının karşısında olacağı anlamına gelir. Köşegenlerle oluşturulan üçgenlerin kenarlarının aynı olduğu göz önünde bulundurularak - bunlar paralelkenarın kenarlarıdır, bu kenarlar arasındaki açının derece ölçüsü köşegenin uzunluğunu belirler, formül ile hesaplanır. Başka bir deyişle, paralelkenarın dar açısının değeri köşegen formülüne konulursa, hesap makinesi kısa köşegenin uzunluğunu hesaplar ve geniş açının değeri konulursa - uzun olanı.

Bir açıdan diğerine geçmek için, 180 derecelik fark ve verilen açı kullanılır, böylece hesap makinesi her iki köşegeni de aynı anda hesaplayabilir.

α=180°-β

Paralelkenarın köşegeninin formülünü türetmek için, köşegenin kenarlarla oluşturduğu üçgende kosinüs teoremi kullanılır. Bu tür üçgenlerden herhangi birinde, köşegen paralelkenarın açısının karşısındaki kenardır ve buna göre karesi, üçgenin diğer iki kenarının karelerinin toplamına eşittir(paralelkenarın, bu durumda)aynı kenarların kosinüs ile çarpımının iki katı çıkarılır. Paralelkenarın köşegeninin uzunluğunu bulmak için, hesap makinesi bu ifadenin karekökünü hesaplar.