Діагоналі трапеції
Трапеція є нетрадиційним чотирикутником, у якому дві з сторін – основи трапеції, паралельні одна одній. Якщо провести діагоналі в трапеції, вони утворюють ряд подібних трикутників, і пропорційні відношення їхніх сторін ведуть до основної властивості трапеції, що поєднує діагоналі трапеції та її чотири сторони:
d12+d22=c2+d2+2ab , де a і b – це основи трапеції, а c і d – її бічні сторони.
Ці ж властивості подібних і рівних трикутників, утворених діагоналями, визначають наступні окремі формули для діагоналей трапеції через сторони:
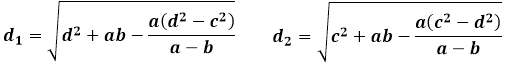
У наведених формулах довжина діагоналі d1 позначає діагональ трапеції, яка утворює трикутник з основою трапеції a і бічною стороною d, а довжина діагоналі d2 дорівнює за значенням, відповідно, до лінії, що з'єднує основу трапеції b і бічну сторону c.
