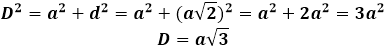Діагональ куба

Куб є базовим геометричним тілом, коли йдеться про об'єм і об'ємні тіла. Не дивно, що третя ступінь, яка виходить при множенні трьох однакових чисел (як при знаходженні об'єму куба - три його однакові виміри) названа на його честь.

Основним і єдиним параметром куба є його ребро a, оскільки всі ребра куба є конгруентними і представляють як довжину, ширину, так і висоту. Відповідно, тільки одне значення визначає всі можливі характеристики куба, пов'язані з його розмірами.

Крім ребер, вершини куба можуть бути з'єднані діагоналями. Діагоналі можуть проходити через грані куба, у такому разі вони просто будуть діагоналлю основи або квадратною діагоналлю в площині, або діагоналі можуть бути проведені всередині самого куба, з'єднуючи протилежні основи в крайніх точках (вершинах).

Щоб знайти діагональ куба через його ребро, спочатку потрібно зробити додаткову конструкцію у формі діагоналі однієї з з'єднаних основ, тоді діагональ куба стає гіпотенузою новоутвореного прямокутного трикутника, катетами якого є ребро куба і діагональ основи. Якщо ребро куба задане умовами задачі, то діагональ квадрата на основі спочатку потрібно обчислити за формулою: d=a√2

Тоді діагональ куба можна виразити через теорему Піфагора, і вона прийме наступний вигляд: