Addition von Brüchen
Addition von Brüchen mit gleichen Nennern:
Definition: Die Summe von Brüchen mit gleichen Nennern wird als ein Bruch bezeichnet, dessen Zähler gleich der Summe der Zähler der ursprünglichen Brüche ist, mit einem Nenner gleich dem Nenner beider Brüche.Formel
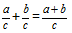
Lassen Sie uns zwei Brüche mit gleichen Nennern addieren
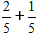
Nach der Formel addieren wir die Zähler und behalten den Nenner bei
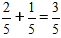
Wichtig: Wenn möglich, schreiben wir den vereinfachten Bruch in die endgültige Antwort.
Beispiel:
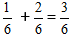Beim Vereinfachen des Bruchs erhalten wir die Zahl 1/2 Addition von Brüchen mit verschiedenen Nennern:
Definition: Um die Summe von Brüchen mit verschiedenen Nennern zu finden, bringen Sie die Brüche zuerst auf einen gemeinsamen Nenner und addieren Sie sie dann wie Brüche mit gleichen Nennern.Aufgabe:
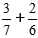
Lösungsprozess:
1) Wir bringen die Brüche auf einen gemeinsamen Nenner.
Dazu finden wir kgV - kleinstes gemeinsames Vielfaches, für Nenner 7 und 6 ist diese Zahl 42.
Teilen Sie die Zahl 42 durch die Nenner der Brüche 3/7 und 2/6
So haben wir die zusätzlichen Multiplikatoren gefunden.
Als nächstes multiplizieren wir die Brüche mit den zusätzlichen Multiplikatoren und erhalten den Ausdruck:
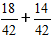
2) Addieren Sie die Brüche.
In unserem Fall kann der Bruch durch 2 vereinfacht werden, und in der endgültigen Antwort schreiben wir die Zahl 16/21
Addition eines Bruchs und einer ganzen Zahl:
Definition: Um einen Bruch zu einer ganzen Zahl hinzuzufügen, stellen Sie die ganze Zahl zuerst als Bruch mit einem Nenner gleich 1 dar.Berechnungsalgorithmus:
1) Wir bringen die Brüche auf einen gemeinsamen Nenner.
2) Addieren Sie die Brüche
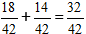
3) Wenn möglich, vereinfachen Sie den resultierenden Bruch.
4) Wenn das Ergebnis ein unechter Bruch ist, berechnen Sie den ganzzahligen Teil davon.
Beispiel:
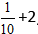
Lösung:
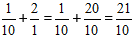
Berechnen Sie den ganzzahligen Teil und erhalten Sie die Antwort
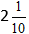
Addition von gemischten Brüchen:
Definition: Um gemischte Brüche zu addieren, müssen Sie die ganzzahligen Teile separat addieren und die Bruchteile separat addieren.Formel
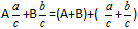
Beispiel:
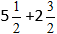
Setzen Sie die Zahlen in die Formel ein:
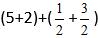
Wir erhalten:
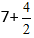
Aus dem Bruch berechnen Sie den ganzzahligen Teil, da er unecht ist, und erhalten den Ausdruck 7+2=9.