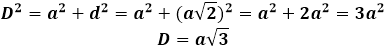Kuution lävistäjä

Kuutiosta tulee perusgeometrinen kappale, kun puhutaan tilavuudesta ja kolmiulotteisista kappaleista. Ei ole yllättävää, että kolmas potenssi, joka saadaan kertomalla kolme samanlaista lukua keskenään (kuten löydettäessä kuution tilavuus - kolme sen samanlaista mittausta) on nimetty sen kunniaksi.

Kuution pää- ja ainoa parametri on sen reuna a, koska kaikki kuution reunat ovat yhteneviä ja edustavat sekä pituutta, leveyttä että korkeutta. Vastaavasti vain yksi arvo määrittää kaikki mahdolliset kuution mittoihin liittyvät ominaisuudet.

Reunojen lisäksi kuution kärjet voidaan yhdistää lävistäjillä. Lävistäjät voivat kulkea kuution sivujen läpi, jolloin ne ovat vain peruslävistäjä tai neliön lävistäjä tasossa, tai lävistäjät voidaan piirtää itse kuution sisäpuolelle, yhdistäen vastakkaiset kannat ääripisteissä (kärjissä).

Löytääksesi kuution lävistäjän sen reunan kautta, sinun on ensin tehtävä lisärakenne muodostaen yhden liittyvän kannan lävistäjä, jolloin kuution lävistäjästä tulee vasta muodostetun suorakulmaisen kolmion hypotenuusa, jonka kateetit ovat kuution reuna ja kannan lävistäjä. Jos kuution reuna on annettu tehtävän ehdoissa, kannan neliön lävistäjä on ensin laskettava kaavalla: d=a√2

Sitten kuution lävistäjä voidaan ilmaista Pythagoraan lauseen avulla, ja se saa seuraavan muodon: