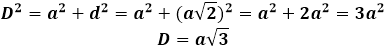Diagonale du Cube
Un cube est un corps géométrique fondamental en ce qui concerne le volume et les corps volumétriques. Il n'est pas surprenant que la troisième puissance, obtenue en multipliant trois nombres identiques ensemble (comme lors de la recherche de le volume d'un cube - trois de ses mesures identiques) porte son nom.
Le paramètre principal et unique du cube est son arête a, puisque toutes les arêtes d'un cube sont congruentes et représentent à la fois la longueur, la largeur et la hauteur. En conséquence, une seule valeur détermine toutes les caractéristiques possibles du cube liées à ses dimensions.
En plus des arêtes, les sommets du cube peuvent être connectés par des diagonales. Les diagonales peuvent traverser les faces du cube, auquel cas elles seront simplement la diagonale de la base ou la diagonale du carré dans le plan, ou les diagonales peuvent être tracées à l'intérieur du cube lui-même, reliant les bases opposées aux points extrêmes (sommets).
Pour trouver la diagonale du cube à travers son arête, vous devez d'abord faire une construction supplémentaire sous la forme de la diagonale de l'une des bases connectées, puis la diagonale du cube devient l'hypoténuse du triangle rectangle nouvellement formé, dont les jambes sont l'arête du cube et la diagonale de la base. Si l'arête du cube est donnée par les conditions du problème, alors la diagonale du carré à la base doit d'abord être calculée en utilisant la formule : d=a√2
Ensuite, la diagonale du cube peut être exprimée à travers le théorème de Pythagore, et elle prendra la forme suivante :