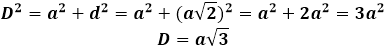Diagonale del Cubo

Un cubo è un corpo geometrico di base quando si tratta di volume e corpi volumetrici. Non sorprende che la terza potenza, che si ottiene moltiplicando tre numeri identici insieme (come quando si trova il volume di un cubo - tre delle sue misure identiche) è chiamata in suo onore.

Il parametro principale e unico del cubo è il suo spigolo a, poiché tutti gli spigoli di un cubo sono congruenti e rappresentano sia la lunghezza, la larghezza che l'altezza. Di conseguenza, solo un valore determina tutte le possibili caratteristiche del cubo relative alle sue dimensioni.

Oltre agli spigoli, i vertici del cubo possono essere collegati da diagonali. Le diagonali possono passare attraverso le facce del cubo, in tal caso saranno semplicemente la diagonale della base o la diagonale del quadrato nel piano, oppure le diagonali possono essere tracciate all'interno del cubo stesso, collegando basi opposte in punti estremi (vertici).

Per trovare la diagonale del cubo attraverso il suo spigolo, è necessario prima fare una costruzione aggiuntiva sotto forma della diagonale di una delle basi connesse, quindi la diagonale del cubo diventa l'ipotenusa del triangolo rettangolo appena formato, i cui cateti sono lo spigolo del cubo e la diagonale della base. Se lo spigolo del cubo è dato dalle condizioni del problema, allora la diagonale del quadrato alla base deve essere calcolata prima utilizzando la formula: d=a√2

Quindi la diagonale del cubo può essere espressa attraverso il teorema di Pitagora, e prenderà la seguente forma: