Dodawanie Ułamków
Dodawanie Ułamków z Tymi Samymi Mianownikami:
Definicja: Suma ułamków z tymi samymi mianownikami to ułamek, którego licznik jest równy sumie liczników oryginalnych ułamków, z mianownikiem równym mianownikowi obu ułamków.Formuła
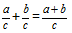
Dodajmy dwa ułamki z tymi samymi mianownikami
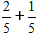
Zgodnie z formułą dodajemy liczniki, a mianownik pozostaje taki sam
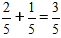
Ważne: Jeśli to możliwe, zapisujemy uproszczony ułamek w ostatecznej odpowiedzi.
Przykład:
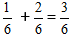 Podczas upraszczania ułamka otrzymujemy liczbę 1/2
Podczas upraszczania ułamka otrzymujemy liczbę 1/2 Dodawanie Ułamków z Różnymi Mianownikami:
Definicja: Aby znaleźć sumę ułamków z różnymi mianownikami, najpierw sprowadzamy ułamki do wspólnego mianownika, a następnie dodajemy je jako ułamki z tymi samymi mianownikami.Zadanie:
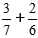
Proces rozwiązania:
1) Sprowadzamy ułamki do wspólnego mianownika.
W tym celu znajdujemy NWW - Najmniejsza Wspólna Wielokrotność, dla mianowników 7 i 6 ta liczba to 42.
Dzielimy liczbę 42 przez mianowniki ułamków 3/7 i 2/6
W ten sposób znaleźliśmy dodatkowe mnożniki.
Następnie mnożymy ułamki przez dodatkowe mnożniki i otrzymujemy wyrażenie:
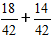
2) Dodajemy ułamki.
W naszym przypadku ułamek można uprościć przez 2, a w ostatecznej odpowiedzi zapisujemy liczbę 16/21
Dodawanie Ułamka i Liczby Całkowitej:
Definicja: Aby dodać ułamek do liczby całkowitej, najpierw przedstawiamy liczbę całkowitą jako ułamek z mianownikiem równym 1.Algorytm Obliczeń:
1) Sprowadzamy ułamki do wspólnego mianownika.
2) Dodajemy ułamki
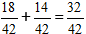
3) Jeśli to możliwe, upraszczamy otrzymany ułamek.
4) Jeśli wynik to ułamek niewłaściwy, obliczamy z niego całą część.
Przykład:
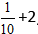
Rozwiązanie:
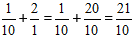
Obliczamy całą część i uzyskujemy odpowiedź
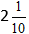
Dodawanie Ułamków Mieszanych:
Definicja: Aby dodać ułamki mieszane należy oddzielnie dodać części całkowite i oddzielnie części ułamkowe.Formuła
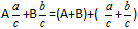
Przykład:
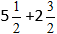
Podstawiamy liczby do formuły:
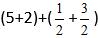
Otrzymujemy:
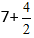
Z ułamka obliczamy całą część, ponieważ jest niewłaściwy, i otrzymujemy wyrażenie 7+2=9.
