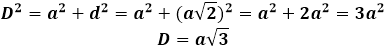Diagonala Cubului
Un cub este un corp geometric de bază când vine vorba de volum și corpuri volumetrice. Nu este de mirare că la a treia putere, care se obține prin înmulțirea a trei numere identice (ca la găsirea volumului unui cub - trei dintre măsurătorile sale identice) este numită în onoarea sa.
Parametrul principal și unic al cubului este muchia sa a, deoarece toate muchiile unui cub sunt congruente și reprezintă atât lungimea, lățimea, cât și înălțimea. În consecință, o singură valoare determină toate caracteristicile posibile ale cubului legate de dimensiunile sale.
În plus față de muchii, vârfurile cubului pot fi conectate prin diagonale. Diagonalele pot trece prin fețele cubului, caz în care ele vor fi pur și simplu diagonala bazei sau a pătratului în plan, sau diagonalele pot fi trasate în interiorul cubului însuși, conectând bazele opuse la puncte extreme (vârfuri).
Pentru a găsi diagonala cubului prin muchia sa, trebuie mai întâi să faceți o construcție suplimentară sub forma diagonalei uneia dintre bazele conectate, atunci diagonala cubului devine ipotenuza triunghiului dreptunghic nou format, ale cărui catete sunt muchia cubului și diagonala bazei. Dacă muchia cubului este dată de condițiile problemei, atunci diagonala pătratului de la bază trebuie mai întâi calculată folosind formula: d=a√2
Atunci diagonala cubului poate fi exprimată prin teorema lui Pitagora, și va lua următoarea formă: