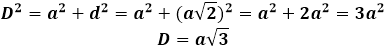Đường Chéo Hình Lập Phương

Hình lập phương là một hình học cơ bản khi nói đến thể tích và các hình thể tích. Không có gì ngạc nhiên khi lũy thừa ba, được tạo ra bằng cách nhân ba số giống nhau với nhau (như khi tìm thể tích của hình lập phương - ba kích thước giống nhau của nó) được đặt tên theo nó.

Tham số chính và duy nhất của hình lập phương là cạnh của nó a, vì tất cả các cạnh của hình lập phương đều bằng nhau và đại diện cho cả chiều dài, chiều rộng và chiều cao. Do đó, chỉ cần một giá trị để xác định tất cả các đặc điểm có thể có của hình lập phương liên quan đến kích thước của nó.

Ngoài các cạnh, các đỉnh của hình lập phương có thể được kết nối bằng các đường chéo. Các đường chéo có thể đi qua các mặt của hình lập phương, trong trường hợp đó chúng sẽ chỉ là đường chéo của đáy hoặc đường chéo hình vuông trong mặt phẳng, hoặc các đường chéo có thể được vẽ bên trong chính hình lập phương, kết nối các đáy đối diện tại các điểm cực (đỉnh).

Để tìm đường chéo hình lập phương thông qua cạnh của nó, trước tiên bạn cần thực hiện một xây dựng bổ sung dưới dạng đường chéo của một trong những đáy kết nối, sau đó đường chéo hình lập phương trở thành cạnh huyền của tam giác vuông mới được hình thành, các chân của nó là cạnh của hình lập phương và đường chéo của đáy. Nếu cạnh của hình lập phương được đưa ra theo điều kiện của bài toán, thì đường chéo hình vuông tại đáy phải được tính trước bằng công thức: d=a√2

Sau đó, đường chéo hình lập phương có thể được biểu diễn thông qua định lý Pythagoras, và nó sẽ có dạng sau: